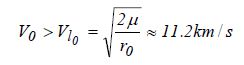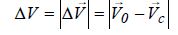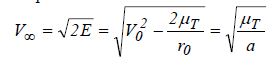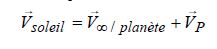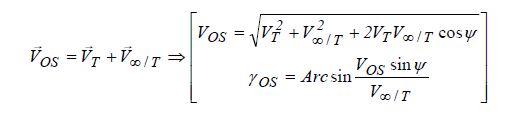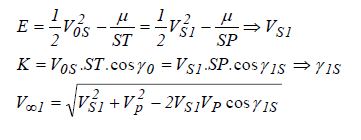بـسم الله الرحــمن الرحـيم
لمحـة تـاريخية :كان الصينيون القدماء أول من اكتشف البارود و خصائصه المميزة و كانوا يستغلونه في إطلاق الألعاب النارية منذ القرن التاسع للميلاد ، و كانوا و بعدهم الهنود و العرب من اول من استخدم صواريخ بدائية في حروبهم عبر اطلاق رماح مدفوعة بمسحوق البارود ، و كانت في جيوشهم وحدات خاصة لإطلاق الرماح الصاروخية ،و سجل استخدامها الأبرز في معركة كاي كينغ 1232 م ،حيث انتصر الصينيون على المغـول نتيجة براعتهم في استخدام صواريخ بدائية كانت تسمى "رمـاح النار".. أما في أوروبا فكان للمسلمين في الاندلس و المغرب الاقصى سبق استخدام البارود و مركبات أخرى في حروبهم خصوصا في المدافع فقد سجل ذكره في مخطوطات اندلسية منذ القرن 10 ، كما جرى استعمال المدافع في حصار سجلماسة على يد سلطان المغرب ابي يوسف يعقوب المريني عام 1273 م .. و قد تأثرت بهم شعوب اوروبا الأخرى، فقد استخدم الفرنسيون الرماح النارية في القرن الـ 15 مع جيش جان دارك ضد الأنجليز في معركة اورليانز ، و في حروب نابليون ضد مقاطعة بولونيا الايطالية 1806 سجل إطلاق 200 صاروخ بدائيا برأس متفجر أدت لاحتراق عدة منازل ...
لكن مع تطور المدافع المحلزنة و دقتها العالية و قوتها التدميرية الأكبر ، جرى تهميش سلاح المقذوفات الصاروخية في الجيوش الغربية آنذاك ،فقد كانت مقذوفات بدائية من دون توجيه و بمدى صغير جدا و قوة تدميرية صغيرة، مع ذلك فهذا لم يمنع البعض من الهوس بدراسة و ابتكار أساليب جديدة و إعطاء معادلات رياضية دقيقة تحكم مفاهيم الدفع الصاروخية ، سواء نظريا أو عملياتيا ، و كــان منهم العالم الروسي كوسطانيتين تسيولكوفسكي الذي يعد من الرواد الأوائل في وضع الأسس النظرية لعلوم الصـواريـخ ، و اليه يعود الفضل في تطور أنظمة الدفع الصاروخية و الفضائية ، فقد تخيل في كتابه "الفضاء الحر" الذي نشر في 1883 رحلات صاروخية الى القمر ، مستندا الى نجاحه في إعطائنا النظرية الأساسية للدفع الصاروخي و التي تسمى لحد الآن باسمه : "معـادلة تسيولكوفسكي"
في بداية القرن العشرين ظهر العديد من العلماء المهتمين بتطوير المشاريع الصاروخية في عدة دول غربية ، من ضمنهم الفرنسي روبيرت بيلتيري و الأمريكي روبيرت غودارد الذي كان له الفضل في البدايات العملية لتطوير الصواريخ تماشيا مع الأسس العلمية و الفيزيائية الحديثة في منتصف عشرينيات القرن العشرين ، لكن في ألمانيا كان الاهتمام الأكبر بالصواريخ ففي ثلاثينيات القرن العشرين ظهر هوس كبير بالصواريخ لدى الألمان مدفوعا بالقرار السياسي و العسكري للقيادة الألمانية ، فكانت أبحاث العالم الألماني هيرمان اوبيرث و فيـرنـر فـون بـراون قاعدة أولى لما سيأتي من صواريخ V1 و V2 الشهـيرة ...
في الاتحاد السوفياتي أضحت أبحاث تسيولكوفسكي مبعث اهتمام كبير في اوساط الطبقة العلمية السوفياتية عكس ما كان عليه من تهميش في العهد القيصري ، و من الرواد السوفييت : المهندسان تساندير و ستيتشكين اللذان نجحا في تصميم محركات دفع صاروخي بدعم حكومي من مؤسسة المواصلات الفضائية التي أنشأت منذ 1924 …
المبادئ العلمية و التقنية الأساسية للدفع الصاروخي :
"لكل فعل رد فعل مساو في الشدة و معاكس في المنحى " .. إنه ببساطة قانون نيوتــن الثالث للحركة ، و ما يجري للصواريخ يعتمد أساسا على هذا المبدأ، فلنتخيل علبة مغلقة بإحكام و وسطها ننتج انفجارا صغيرا يمكن لجدرانها الداخلية تحمله دون ان تنفجر ... الانفجار يتبعه موجة ضغط صغيرة تصطدم بالجدران الداخلية للعلبة ... لكن العلبة لن تتحرك لأن مقدار الضغط عند كل جانب يكون مساويا للضغط في الجانب المقابل .. بعدها نحدث ثقبا في أحد الجوانب ، الذي سيحدث عندئذ أن مقدارا من الهواء المضغوط سيخرج من العلبة و بالتالي فإن جدار الجانب الذي فيه ثقب سيستقبل ضغطا أقل من الجانب المقابل ، ما سينتج عنده حركة للعلبة في منحى الجدار المقابل للثقب ...
و منـه فإنه من البديهي أن الصاروخ و القوة الدافعة له ستكون متعلقةبكمية الهواء الخارج و سرعة خروجه من عادم المحرك الدافع ... و هو ما يتوافق مع مبدأ انحفاظ كمية الحركة :
m(t).dv= dm.Ve
m(t) كتلة الصاروخ في اللحظة t ،
dm كتلة الوقود المحترق خلال زمن متناه الصغر dt ،
dv تغيـرسرعة الصاروخ خلال لحظة dt
Ve سرعـة الهواء الخارج من المحرك
المعادلة هنا تصف التوافق بين تغير سرعة الصاروخ و تغير كتلته و سرعة نفث الهواء المحترق ، إنها بداية معادلــة تسيولكوفسكي الأسـاسية ...
فالـقوة المتولدة عن ذلك يمكن كتابتها على شكل اشتقاق زمني لكمية الحركة كــالآتي
F = dP/dt = (dm/dt )* V
حيث كمية الحركة تساوي P = m.V
في الظروف الواقعية تكون الصيغة الاجمالية لقوة الدفع المتولدة كما يلي :
F = dm/dt * Ve + As* (Ps - Pext)
As مسـاحة قاعدة الـ Nozzle الخارجيـة
Ps - Pext الفرق بين الضغط داخل عادم المحرك Nozzle و الضغط الخارجي ..
و بالرجوع الى مبدأ انحفاظ الحـركة نجد أن التغير في سرعة الصاروخ بين اللحظة البدئية و النهائية هو بحساب التكامل على الشكل الآتي :
Ve سرعة نفث الغاز المحترق ، m0 الكتلة الإجمالية الأولية ، mf الكتلة الإجمالية النهائية .
ln دالة اللوغاريتم النيبيري
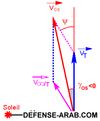
المعادلة هنا تخص الصاروخ في الوضع المعزول عن أي قوة عدا قوة دفعه الخاصة (حالة الدفع في الفضاء الخارجي) ، لكن مع الإطلاق الأرضي يكون على الصاروخ الوصول الى قوة دفع أكبر ، تفرضها عليه الجاذبية الأرضية و الغلاف الجوي الأرضي ، فبوجود قوة الجذب الأرضي ، تكتب المعادلة على الشكل التالي:
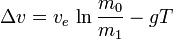
حيث g0 هي تسارع الجاذبية عند سطح الأرض (9.81 م\ث 2) : ( التعبير هنا مبسط لأن تسارع الثقالة يتغير مع الارتفاع و مع تغير خط العرض).. و T زمن التسلق الرأسي للصاروخ .. لكن في الواقع فان خسارة السرعة تقل تدريجيا مع الارتفاع لأن تسارع الجاذبية يقل ولو بشكل ضئيل كلما ابتعدنا عن الأرض و كذا فإن تأثير الغلاف الجوي يكاد ينعدم عند 100 كلم من سطح الأرض و منه يتضح أن السرعة الفعلية التي يصلها صاروخ مطلق من الأرض هي أقل من السرعة التي كان بإمكانه وصولها في حالة معزولة عن القوى الخارجية .. فالصاروخ يخسر حوالي 1 الى 1.5 كلم \ث نتيجة الاحتكاكات.. و بالنسبة لصاروخ معد لإطلاق قمر في مدار بارتفاع 200 كلم و يستغرق 240 ث للوصول الى المدار .. فإن السرعة التي يجب على محركه العمل على توفيرها ليضع قمرا بسرعة فعلية 8 كلم \ث هي :
8 +1+2.35 = 11.35km/s
معــامل الدفـع الخاص Isp
الـ Isp معامل فيزيــائي مهم يعطينا فكرة حول أداء المحرك الصاروخي و الوقود المستعمل و هو معبر عنه بالثواني و حسب المعـادلة التاليـة :
Isp = F/ q*g0
حيـث F قوة دفع المحرك بالـنيوتن ، q هنا تشــير الى الصبيب الكتلي q= dm/dt
و g0 تمثل تسـارع الثقالة عند سطح الأرض
الـ Isp يمثل في الواقع المدة اللازمة ل 1 كلغ من المادة الدافعة لاعطائنا 1 كلغ قوة أو 9,81 نيوتن ، حيث أنه كلما ارتفع الـ Isp لمحرك معين كان اكثر مردودية و أفضل من ناحية الاستهلاك فعند قوة دفع ثابتة لمجموعة من المحركات بـIsp مختلف ، ازدياد هذا الاخير من محرك A لاخر B مثلا، يعني بالضرورة ان q تنخفض .. أي أننا لن نكون بحاجة الى صبيب كتلي كبير للمحرك B مقارنة بـ A للحصول على نفس القوة F
كما أن Isp تحدده عدة عوامل منها أساسا نوعية الوقود المستخدم ثم تصميم المحرك و الضغط المتولد داخله حيث يستطيع العامل الأخير التاثير بنسبة 10 الى 15 % من Isp الخاص بالمحـرك
وقــود و محركات الدفـع الصاروخــي
محركات الوقــود الصلــب :

محركات الدفع بالوقود الصلب تحتوي على وقود مركــب على شكل بودرة ممزوجة بمادة رابطة تعطيها طبيعتها الصلبة و شكلها الملائم ونجدها على شكل بوليمير قابل للاشتعال كعـديدات و مشتقات البيوتادين و الأكريلونيتريل ، و يكون الخليط محتويا على نسب عالية من مؤكسد احتراق صلب ، عـادة ما يكون على شكل بيركلورات أو نيترات و هي مواد مشبعة بالأوكسيجين ، اضافة الى مختزل عادة ما يكون معدنيا كـالالومينيوم و الكبريت و المنغنيزيوم و غيره ..
من أنواع الوقود الصـلب الاكثر شيوعـا للمهمات الفضائية وللصواريخ البالستية العاملة على الوقود الصلب و حتى بعض الصواريخ التكتيكية و صواريخ جو-جو : الوقود المركب لبركلورات الامونيوم APCP و الذي يستخدم في SRB لدفع المكوك الفضائي الامريكي و ايضا في معززات Vulcan للصاروخ الاوروبي Ariane 5 ، يتالف هذا الوقود المركب من نسبة 60-70 % من بيركلورات الأمونيوم NH4ClO4 ، و حوالي 15 - 20 % من الألومينيوم ، و النسبة المتبقية من مادة PBHT poly butadiene hydroxytelechelic الرابطـة يصلIsp لهذا الخليط الى 270 ثانية في الفراغ، كما يمكن اضافة نسبة مدروسة من متفجرات RDX و HMX للوصول بالخليط الى Isp يقـارب 300 ثانية .. تضاف أيضا محفزات للتفاعل بمقدار 0.2 - 0.4 % من اوكسيد الحديد Fe2O3 غالبا او ثنائي اوكسيد المنغنيز MnO2 او حتى ديكرومات النحاس CuCr2O7 ..
أنــواع اخرى من الوقود الصلب استخدمت و لا تزال كخليط نيترات الأمونيوم مع مزيج من المواد النفطية و الالومينيوم ANCP الذي يبلغ Isp 210 ثانية .. و بيركلورات البوتاسيوم KClO4 و الأسفالت كوقود و مادة رابطة ..
الوقود ثنائي القاعدة النيتروسيليلوز/ النيتروكليسيرين يعطي Isp بقيمة قد تصل احيانا الى 225 ثانية ، و منـه مركبات دافعة لقذائف المدفعية مثل الكورديت و البالستيت ، و ايضا مركبات لبعض الصواريخ التكتيكية و الصواريخ المضادة للدروع..
الصواريخ التجريبية او صواريخ الهواة لها طيف واسع من انواع الوقود الرخيص و المتوفر بسهولة كالبارود ( نيترات البوتاسيوم + الكبريت و الفحم) بـ Isp ضعيف يصل الى 80 ثانية ، و الوقود السكري المكون من نيترات البوتاسيوم كمؤكسد و وقود من الساكاروز او الكلوكوز و يعطي Isp يصل الى 130 ثانية.. اضافة الى نيترات الأمونيوم/ السوربيتول بـ Isp يقارب 200 ثانية ..
يتألف المحرك بشكل مبسط من غلاف خارجي يضم المكونات الاساسية للدفع و عادة ما يكون مصنوعا من الفولاذ أو من ألياف الكربون و التيتانيـوم لتحمل الضغوط العالية الداخلية الناتجة عن احتراق الوقود الصلب ، داخل الصاروخ نجد المادة المتفاعلة(مؤكسدات و مختزلات التفاعل) مجوفة داخليا ، ذلك التجويف يمثل غرفة الاحتراق .. في اعلى غرفة الاحتراق نجد موقدات التفاعل و في الأسفل عادم الصاروخ (nozzle) حيث تكون مصممة بشكل دقيق لزيادة سرعــة نفث المتفاعلات و بالتالي الوصول بالصاروخ الى سرعات أكبر ..
محركات الدفع بالوقود الصلـب تعطي دفــعا كبيرا في وقت قصير.. كما ان تكاليف تصميم و بناء محركات الوقود الصلب أقل ، و وقودها قابل للتخزين غالبا في الظروف العادية للحرارة و الضغط و لـوقت طويل ما يجعلها الخيار الأول لصواريخ الميدان عالية السرعـة و أيضا لمعززات الدفع للصواريخ الفضائية .. إلا أن Isp الخاص بها ضعيف مقارنة بمحركات الوقود السائل ما يعني أن دفعها لا يكون مستمرا لفترات طويلة و غير مناسب للمهمات الفضائية المتطلبة لفترات دفع اطول ..
هندســة غرفة الاحتراق :
تمثل غرفة الاحتراق و شكلها عاملا أساسيا في مميزات دفع الصاروخ حيث أن احتراق المادة الدافعة يتم على سطح تجويف غرفة الاحتراق و الذي يكبر حجمه مع استنفاذ المادة المتفاعلة ..السبب الرئيسي هو في اختلاف مساحة التفاعل بين شكل و آخر و بالتالي اختلاف في تغير كتلة المادة المتفاعلة مع الزمن الشيئ الذي يعني اختلافا في مستويات الدفع .. و تعبر عنه المعادلة التالية :
dm/dt = ρ.As .br
As مساحة الوقود المحترق في اللحظة t
ρ الكتلة الحجمية للوقود
br و هي سرعة الاحتراق أو burn rate بالانجليزية
هنــاك عدة أشكال لتجاويف غرفة الاحتراق و الأكثر استخداما هي الآتية :
التجويف الاسطواني التماثلي : هو النمط الهندسي الأقل تعقيدا لكنه يعطينا نمط دفع تصاعدي ثم ما يلبث ان يتناقص مع الزمن .. كما انـه غالبا لا تتم المحافظة على الشكل الأسطواني في غضون الاحتراق ما يعطي دفعا غير ثابت ..
تجويـف C-Slot : حيث يتم وضع التجويف في طرف غرفة الاحتراق ما يعني ان الاحتراق لا يكون تماثليا ، ينجم عن هذا النمط دفع تصاعدي ثم تنازلي ، لكن تغير قيم منحنى الدفع تكون أبطأ .. ما ينجم عنه دفع قوي لمدة أطول لكن في المقابل يعطي هذا النمط الهندسي مشاكل في الاستقرار الحراري و تغيرا في مركز ثقل الصاروخ ناجم عن عدم التماثل ..
التجويـف النجمـي : يعتبر هو و مشتقاته النمط الهندسي الأكثر استخداما في غرف احتراق الصواريخ الحديثة ، و يكون عبارة عن نجمة بـ 5 الى 8 رؤوس عادة و الهدف من هذا الشكل هو توفير مساحة اكبر للاحتراق ما ينعكس ايجابا على منحنى الدفع فننتقل بعد أجزاء من الثانية من تصاعد سريع للدفع الى استقرار في قيمة الدفع لمـدة طويلة من الزمن ..
معـززات الصاروخ الفضائي Ariane 5 و كذا الـ Space Shuttle الأمريكي تستخدم أنماطا مركبة عبر Blocks ففي البلوك الاعلى نجد تجويفا نجميا سداسيا يحترق أولا عند تشغيل الصاروخ مانحا اياه قيمة دفع كبيرة ثابتة لمدة طويلة .. ثم البلوك الاوسط يتألف من تجويف اسطواني ثم نجد تجويفا مخروطيا في البلوك الاخير الذي يشتعل في المرحلة الاخيرة من الدفع الصلب حيث يتخلص بعدها الصاروخ من معززاته ليبقـى معتمدا بعدها على محركاته العاملة على الوقود السائل ..
مكونات المحـرك الصاروخي بالوقود السائل
بالنسبة للصواريخ العاملة على الوقود السائل فإن عدة محرك الصاروخ تكون مؤلفة من عدة مكونات أساسية من أهمها :
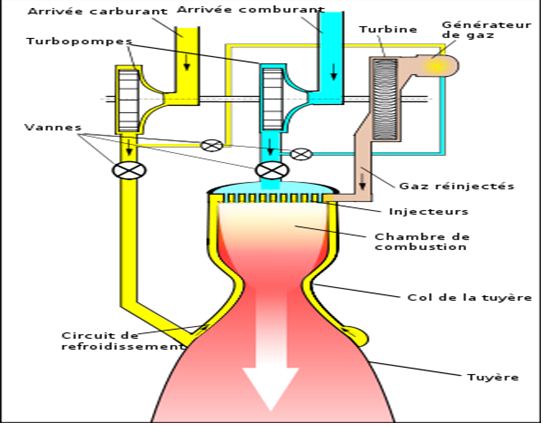
خزانات الوقود : و التي يتم فيها تخزين المادة المحترقة و كذا غالبا المادة المؤكسدة و اللتين تشكلان أغلب كتلة الصـاروخ ، و هي غرف تخزين يتم ضبطها على درجات حرارة و ضغط معينة ، و يراعى فيها مخاطر التسرب و تحمل الصدمات و كذا الكتلة الصغيرة للخزانات ما يستوجب صناعتها من مواد تجمع بين الخفة و التحمل .. و عادة ما تتكون من الألومينيوم و ألياف الكربون .. و تكون موصولة بأنابيب ضخ تصل الوقود الصاروخي بمضخات في محرك الصاروخ .
مضخات الوقود : و هي مضخات تقوم بضخ الوقود و المؤكسد الى غرفة الاحتراق و كذا ضخ الوقود السائل في جدار غرفة الاحتراق بغية تبريدها و خفض حرارتها الشديدة الارتفاع ..
غرفة الاحتراق : فيها يلتقي الوقود بالمؤكسد و قد تحتوي على أجهزة لبدء الاشتعال و قد لا تحتوي حسب طبيعة الوقود المستخدم ، و هناك يحدث الاحتراق الذي يعطي ضغطا و حرارة شديدين و يتم نفث الهواء المضغوط و الساخن الى الخارج عبر عادم المحرك Nozzle و الذي يكون بدوره مصمما على شكل مخروط تتباعد جدرانه من غرفة الاحتراق الى الخارج .. و ذلك في سبيل زيادة الضغط المعاكس المتولد عكس منحى نفث الغاز ...
وقــود الدفــع الصاروخي
من خلال المعادلة أعلاه يتبين الحاجـة الى زيادة سرعة نفث المتفاعلات من محرك الصاروخ إذا أردنا أن يحصل هذا الأخير على سرعة نهائية كبيرة ، و لفعل ذلك وجب البحث و تطوير مركبات كيميائية أكثر فاعلية و أكثر أمانا ، فنرى مثلا أن البترول العادي يحترق مع الهواء بـحرارة 2300 درجة مئوية و بسرعة 2000 م\ث ، و مع ثنائي الأوكسيجين بــ 3000 درجة مئوية و بسرعة 2500 م\ث ، أما بالنسبة لاحتراق الهيدروجين مع الفليور فيولد سرعة الاحتراق تصل إلى ما يقارب 4600 م\ث و بحرارة متطرفة قد تصل الى 3600 درجة ..
و بالتالي فإنه كلما زادت سرعة النفث المنشودة ، زادت معها حرارة التفاعل ، الأمر الذي يجعلنا نواجه مشاكل كبيرة أخرى من أبرزها صمود و قوة هيكل المحرك ، و وجوب تبريده باستمرار، فالحديد يذوب عند 1400 درجة و الكروم عند 1800 درجة .. أما المعادن الأكثر تحملا كـالتانغستن و التيتانيوم فتذوب عند حدود 3200 درجة ..هذه المعضلة كانت أكبر المشاكل التقنية التي واجهتها الصواريخ الأولى مثل الـ V 2 و المشتقات الفضائية الأولى للـ R-7 Semyorka رغم أن سرعة نفث محركها لا تتجاوز 2600 م\ث
فالصواريخ العاملة على الوقود السائل هي الخيار الأول لتسيير الرحلات الفضائية الصاروخية فرغم كونه أكثر خطرا و تكلفة إلا أن السرعات التي يصلها و استمرارية دفعه عالية جدا مقارنة بالوقود الصلب ، كما ان دفعه متحكم به فيكفي ايقاف ضخ المواد المتفاعلة الى غرفة الاحتراق لايقاف الدفع و هذا أمر مهم لمحركات المناورات المدارية و الهبوط و الاقلاع من فوق أجرام فضائية اخرى .. فهناك عدة خيارات ممتازة من المركبات .. نذكر منها :
انواع الوقود الازوتي القابل للتخزين لفترات طويلة :
N2O4 / UMDH بيروكسيد الآزوت و ديميثيل الهيدرازين ، له ميزة إمكانية تخزينه في ظروف حرارة و ضغط عاديين و كذا أن هذا الزوج يحترق بالتماس بين مكوناته Hypergolic.. بيروكسيد الازوت يكون ممزوجا مع نسبة ضئيلة من مونوكسيد الأزوت لتفادي مشكل التآكل الذي يسببه في طبقات التيتانيوم المتواجد في هيكل غرفة الاحتراق ، كما أن الـ UMDH مادة سامة جدا و مسرطنة ، بدأ استعماله منذ الستينات في صواريخ Diamant لبرنامج الفضاء الفرنسي ، يستخدم عادة في عمليات الاقلاع الارضية و المراحل الاولى لصواريخ مثل Proton M الروسي و Arian 1/2 الاوروبيان ، يسمح هذا النوع من الوقود بالعمل على محركات اقل تعقيدا و كلفة كما ان تبريد المحرك يتم عبر فرش طبقة متجددة من الوقود على جدران غرفة الاحتراق .. Isp يصل عادة بين 310 – 320 ثانية
Aerozine 50 هو خليط من 50 % من الهيدرازين N2H4 و 50 % من UMDH مع بيروكسيد الازوت ظهر منذ الخمسينات كوقود للصواريخ البالستية Titan 2 ، كما كان مستخدما لمحركات الهبوط و الاقلاع على القمر لرحلات Apollo ، حاليا مستخدمة على محرك المرحلة الثانية من صواريخ دلتا 2 الامريكية بـ Isp يقارب 320 ثانية ..
MMH او مونوميثيل الهيدرازين ممتاز لمهمات التوجيه و تصحيح المسار للمسابير و الاقمار الصناعية في المدارات لاستقراره و فترات خزنه الاطول ، يستخدم مع مؤكسد MON-x و هو خليط من x % من بيروكسيد الازوت و 100- x% من مونوكسيد الازوت ( عادة x بين 1 و 5 ) ..
يمكن للهيدرازين العمل كوقود وحيد كما الحال في العديد من محركات الهبوط فوق الكواكب و تعديل المدار للمسابير و الأقمار الصناعية عبر اضافة محفزات للتفاعل كنيتريد الموليبدن او الايريديوم ما يساهم في تفكك الهيدرازين و انتاج كثيف لغازي الازوت و ثنائي الهيدروجين في عملية كيميائية بطاقة حرارية عالية ، محركات الهيدرازين تصل عادة الى ما فوق 200 ثانية Isp
أنواع الوقود العاملة على ازواج احتراق محفوظة في درجات متدنية Cryogenic اكثر فاعلية و عادة ما يكون الاوكسيجين السائل المؤكسد الاساسي فيها إلا انها تستلزم نظام دفع أعلى كلفة و أعقد تقنيا ..
LOX/ RP1 : RP1 Rocket Propellant 1 و هو نوع خاص عالي التكرير من الكيروسين اضافةللأوكسيجين السائل المحفوظ في حرارة منخفضة تقارب -183 درجة مئوية Cryogenic، و هو أكثر فاعلية و أقل تلويثا من الوقود الازوتي .. و يستعمل بشكل واسع في مراحل دفع صواريخ Soyuz FG الروسية و صواريخ Zenit الاوكرانو- سوفياتية و كذا صواريخ Delta 3 الامريكية و غيرها ، مشتق روسي اخر أكثر كثافة يسمى RG-1 يستعمل على محركات RD-108 للمرحلة الاولى لصواريخ Soyuz 2 .. LOX/RP-1 يعطي قيم Isp بين 270 و 350 ثانية في الفراغ كما انه اكثر سهولة في التخزين و التعامل ومتطلبات تصميم المحركات من الهيدروجين السائل ..
H2/O2 هذا الزوج من الأكثر فاعلية و الذي يمكن استبدال ثنائي الأوكسيجين فيه بالفليور.. فرغم كون المكونين معا في الحالة السائلة ( الهيدروجين عند -253 مئوية و الاوكسيجين -183 ) ما يطرح مشاكل تقنية لحفظ الوقود بالإضافة الى الكثافة المنخفضة للهيدروجين السائل ما يجعل خزانات الوقود تمتلأ بسرعة، إلا أنه الأقل تلويثا فتفاعلهما ينتج عنه الماء فقط ، و احتراق الهيدروجين السائل في الاوكسجين السائل يولد طاقة اعلى في كل وحدة كتلة ..احتراقهما يولد قوة دفع عالية جدا و حفضهما في الحالة السائلة في حرارة منخفضة مكن المهندسين و العلماء من التغلب على مشكل الحرارة العالية في هيكل المحرك ... فتصميم المحرك يحتوي على انابيب صغيرة على جداره بحيث يضخ الوقود السائل فيه باستمرار لانجاز مهمتين ، أولا يتم تبريد حرارة المحرك قدر الإمكان ، ثم يتجه الوقود عبر الأنابيب ليحترق في أعلى غرفة الاحتراق في ما يسمى بالدارة المغلقة ... و هو مستعمل سواء في المكوك الفضائي الأمريكي(Space Shuttle) أو الصاروخ الاوروبي Ariane 5و تعتبر تقنية الدارة المغلقة من الأفكار الفذة للعـالم الألماني فيرنر فـون براون في بداية الأربعينيات .. كفاءة محركات LOX/LH2 تصل الى 412 ثانية Isp للأمريكي RS-68 و 3100 كيلونيوتن ، محرك المرحلة الاولى لصاروخ Delta 4 .. و 452 ثانية للياباني LE-5 محرك المرحلة الثانية للصاروخ H-2 الياباني من انتاج ميتسوبيشي للصناعات الثقيلة ..
الصــاروخ متعدد المراحل : فكرة لامعة
لوضع قمر صناعي على علو 200 كلم مثلا ينبغي الوصول الى سرعة فعلية تصل الى حوالي 8 كلم/ ثانية و على مدار 2000 كلم ينبغي توفير 6.9 كلم/ ثانية ليبقى القمر في مداره حول الارض و تلك سرعات كبيرة جدا لا يمكن وصولها حتى مع أقوى أنواع الوقود في حال صاروخ احادي الطبقات ..
لاعطاء مثال بسيط على ذلك لنتخيل صاروخا كتلة هيكله وأنظمته + كتلة شحنته المراد وضعها في المدار تساوي 600 كلغ و يحمل 3 أطنان من الوقود بسرعة نفث تساوي 3 كلم / ثانية .. معادلة تسيولكوفسكي و مع اهمال تاثير الغلاف الجوي و الثقالة نجد ان DV= 3*ln(3600/600)= 5,3 km/s .. أي ان مع اكثر انواع الوقود سرعة فان مثل هذا الصاروخ لن يوفر لنا سرعة كافية للاستقمار ..
عكس هـذا ،لو فرقنا الكتلة الاجمالية للصاروخ بشكل متساو على 3 مستويات قابلة للفصل مثلا و وزعنا كمية الوقود عليها بالتساوي أيضا ، (اي طن وقود لكل مستوى) فان الامر يختلف ، بحساب بسيط سنجد أن تغير سرعة المستوى الأول DV1= 3*ln(3600/2600)=1,4 km/s
سيتم فصل المستوى الفارغ و ستبدأ المرحلة الثانية من الدفع
DV2= 3*ln(2400/1400)=2.1 km/s
في حين ان المرحلة الثالثة و الاخيرة ستعطي الآتي :
DV 3 = 3*ln(1200/200)=4,8 km/s
و بالتالي التغير الكلي للسرعة سيكون بجمع السرعات في المستويات الثلاثة
DV = 1,4+2,1+4,8 = 8,3 km/s
الفكرة بشكل عام هي تغيير العامل الثاني في المعادلة و هو معامل الكتل البدئية و النهائية و هو ما يتم فعليا في الصواريخ الفضائية و الصواريخ العابرة للقارات لكن بشكل اكثر تعقيدا فعادة تكون المرحلة الأولى الأثقل في جسم الصاروخ و التي تحمل اكبر كمية من الوقود و أكثر عدد من محركات الدفع و المعززات الصاروخية و ذلك لأنها المرحلة التي تشهد أكبر قوى معاكسة للدفع الصاروخي من ناحية كثافة الغلاف الجوي و تأثير الثقالة ، بينما تكون المرحلة الاخيرة و التي تتكلف بالاستقمار المباشر اصغر لأن الشحنة تكون في وضع شبه معزول عن الاحتكاكات بفضل انعدام الغلاف الجوي..
قوانين كيبــلر و سرعات الاستقمار :
قوانين كيبلــر الثلاثة و المنسـوبة لعالم الفلك الألماني يــوهانس كيـبلـر هي القوانين التي تصف حركة الكواكب حول الشمس و بصفة عامة فهي صالحة لكل جسم في مدار حول جرم فلكي ..و تعتبر قواعد اساسية لا بديل عنها في فهم خصائص المدارات للاقمار الصناعية و الأجرام الأخرىلذلك وجب ذكرها أو التذكير بها ولو بشكل مقتضب قبل التوغل أكثر في الموضوع.. تم نشر القوانين عامي 1609 و 1618 .. و كانت نواة ابحاث نيوتن حول قوى التجاذب الكوني و قانونها الشهير الذي نشر عام 1687 ..
قانون كيبلـر الأول :
تتخذ الكواكب مدارات اهليلجية حيث تكون الشمس مركز احدى بؤرتي الاهليلج
قانون كيبلر II
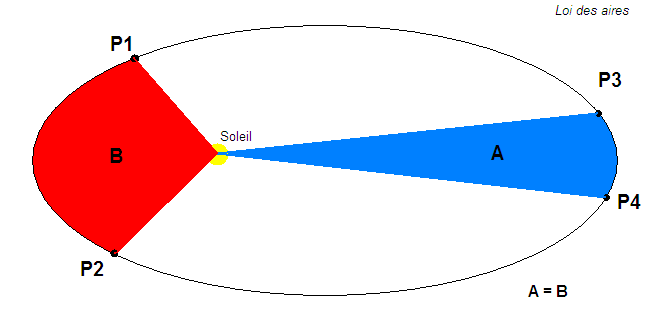
القانون الثاني او قانون المساحات فبأخذ الشمس في احدى البؤرتين و في نفس المدة Dt فان المساحة المحصورة بين القوس P1P2 و بؤرة الاهليلج تعادل المساحة المحصورة بين القوس P3P4و البؤرة التي هي الشمس بالنسبة للنظام الشمسي .. تفسير انحفاظ المساحات هو ان سرعة الكوكب تتغير حسب قربه من الشمس ، فالكواكب تزيد سرعتها باقترابها من الشمس و تنخفض عند ابتعادها عن البؤرة (الشمس)
قانون كيبلر III
و هو قانون تناسب بين مربع الدور المداري و مكعب طول المحور الأكبر للاهليلجو يعبر عنه كالتالي :
a^3 = k.(T/2π)^2
حيث a طول نصف المحور الأكبر للاهليلج ، T الدور المداري و هو الوقت اللازم للكوكب للرجوع الى نفس النقطة من المدار ، k ثابتة تتعلق بالشمس أو بالجرم الذي يتم حوله الدوران عموما ..
نستمر بالمعطيات التالية :
m كتلة الجسم ،Mكتلة الجرم ، D المسافة بين مركزي ثقلهما و V سرعة دوران الجسم
جسم في حالة دوران دائري منتظم حول جرم معين في معلم غاليلي (معزول نظريا) يعني أن هناك توازنا في القوى المؤثرة عليه و بالتالي فمجموع متجهاتها يساوي صفرا ، في هذه الحالة هناك قوتين فقط ، أولاها قوة جاذبية الجرم و المعبر عنها G Mm/D ^2 بينما القوة الثانية هي قوة الطرد المركزي و التي تسعى لخلق توازن مع قوة الجذب وبالتالي منع الجسم من السقوط على الجرم .. فالجسم أثناء دورانه بسرعة منتظمة ينعدم تسارعـه المماس لمسارهaT و لا تبقى إلا قيمة تسارعه المركزيNormal AccelerationaN = V^2/Dو منه فقوة الطرد المركزي تساوي m.V^2/D و عليه فإن
G.M.m/D^2 = m.V^2/D ( الكتابة هنا بمنظم القوتين دون متجهات)
و منـه نجد قيمة سرعته
V = (G.M/D)^(1/2)
و بما أن V = 2π.D/T فإن T = 2π(D^(3/2))/(G.M)^1/2
و منه نرجع الى صيغة قانون كيبلر 3 مع اعتبار a= D المسافة بين مركزي ثقل الجسم في المدار و الجرم ،و k = 1/G.M، حيث G ثابتة كافينديش للتجاذب الكوني و M كتلة الجرم ..
سرعات الإستقمار و التحريـر :
سـرعة الاستقمار هي السرعة الدنيا Vs minالتي يجب اعطاءها لجسم للبقاء في مدار حول الجرم دون سقوطه على السطح ، و حسب التعبير أعلاه فإن البارامتر المتغير بالنسبة لحالة قمر صناعي حول الأرض هو ارتفاع المدار و منه فإن السرعة اللازم إعطاءها له ليبقى في مدار دائري تنقص مع الارتفاع ، ففي مدار 200 كلم مثلا سرعة الاستقمار الدنيا Vs min = 7.86 Km/s ، بينما تصل الى6.15 Km/s لارتفاع 4190 كلم ، و 4.88 Km/s لـ 10400 كلم .. في حيـن تقارب3.07 Km/s على ارتفاع 35800 كلم و هو ارتفاع المدار الأرضي الثابت GEO
مدار قمر صناعي لا يكون دائريا إلا في حـالـة الوصول به الى سرعة الاستقمار الدنيا المكافئة لارتفاع المدار الذي نريد الاستقمار عليه و كذا انفصال القمر الصناعي عن المركبة الحاملة بشكل متواز مع سطح الارض .. في حالـة سرعة استقمار أكبر من Vs min فإن المـدار سيكون اهليلجيا ، بـؤرتـه مركز الأرض و حضيضه في نقطة الانفصال
بالنسبة للمدارات الاهليلجية eliptic orbits فإن سرعة القمر الصناعي تتغيـر حسب موضعه في المدار و بالتالي حسب بعده عن المركز البؤري (الارض) فتصل الى مستواها الاقصى عند الحضيض بينما تهبط الى ادنى مستوى عند الأوج(ابعد نقطة عن الارض) و ذلك ترجمة لانحفاظ الطاقة الميكانيكية للجسم في المدار، و يعبر عنها بالعلاقة التاليـة :
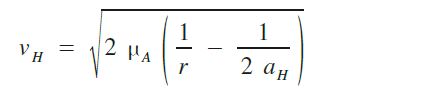
حيث r المسافة بين القمر في المدار و مركز الأرض و a هو نصف القطر الأكبر للاهليلج و المقدار
μA=G.M
..
قد يتبادر الى الذهن تساؤل حول السرعة اللازم اعطاءها لجسم ما ليخرج تماما من الجاذبية الأرضية و ينفلت من حالة الدوران حول الأرض و هو ما يسمى بسرعة التحرير أو Escape Velocity و التي يمكن حسابها عن طريق معادلة انحفاظ الطاقة الميكانيكية للجسم في المدار و يعبر عنها كالآتي :
Vesc = (2.Vs min)^1/2
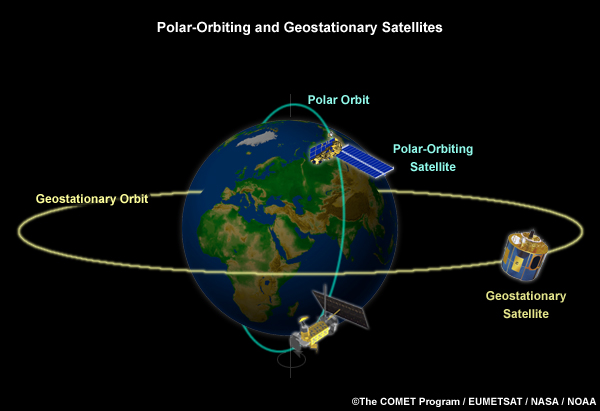
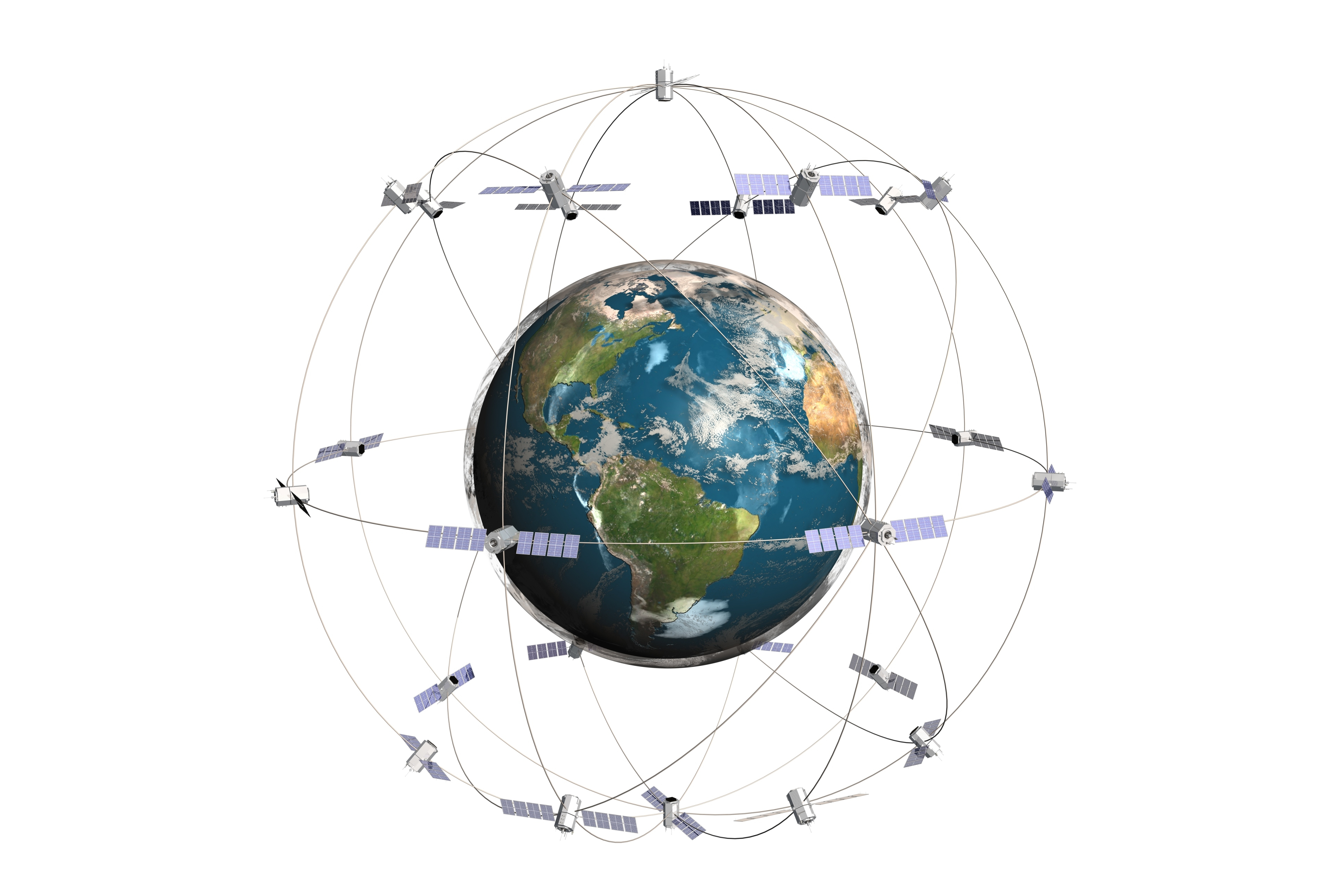
خصــائص المدارات و نـوافـذ الإطلاق
للمـدارات خصائص عديـدة تميزها عن بعضها البعض سواء كانت اهليلجية او دائرية و من أهمها :
_ الدور المداري T و هي المدة الزمنية التي يقوم فيها الجسم بلفة واحدة في المدار و تحسب كما راينا أعلاه بالقانون 3 لكيـبلر ، حيث يتغير حسب نصف قطر الاهليلج a أو شعاع المدار r في حالة المدارات الدائرية فيعطي قيمة 90 دقيقة لقمـر على ارتفاع 200 كلم و 24 ساعة لقمر على ارتفاع 36000 كلم
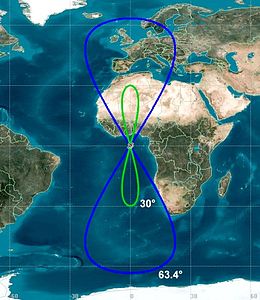
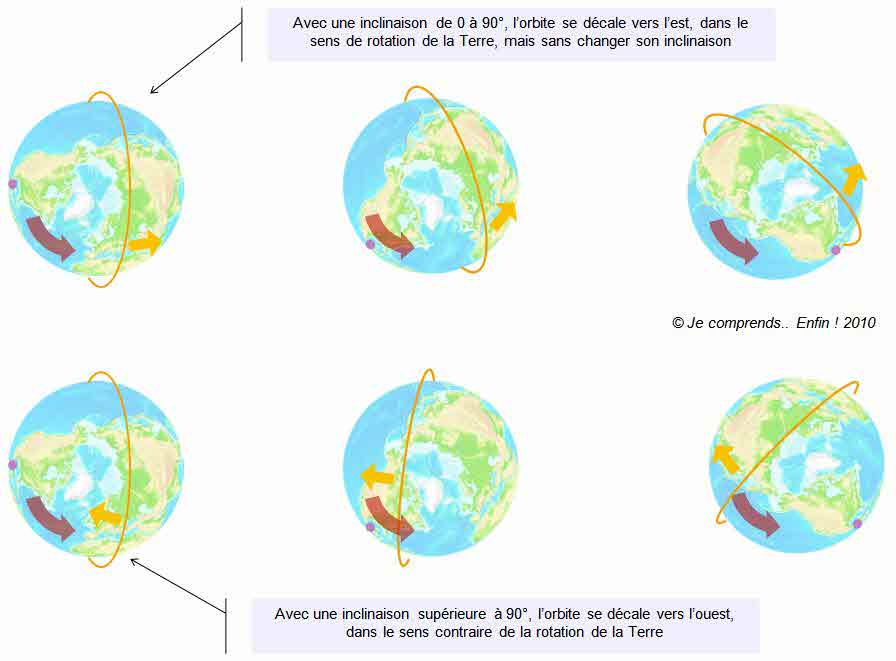
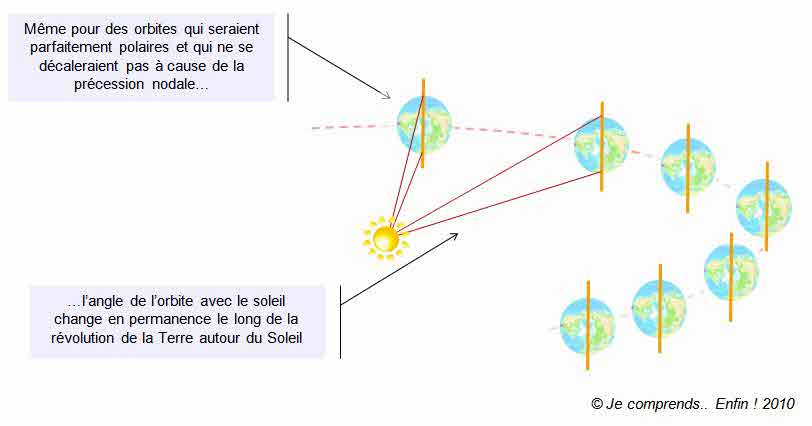
_ زاوية الميل Inclinaison α و هي الزاوية التي يتخـذها مستوى المدار مع مستوى خط الاستواء .. ففي حالـة α≃ 0° نقول ان المدار استوائي بينما يكون المدار قطبيا اذا قاربت زاوية المدار 90 °
_ زاوية الحضيض argument of periapsis ω و هي تؤشر للزاوية بين اتجاه العقدة الصاعدة للمدار و اتجاه حضيض المدار
_ العقد المدارية : الصاعدة و النازلة للمدار و هي النقطتين التي يقطع فيهما المدار مستوى خط الاستواء بالتوالي حسب اتجاه دوران الجسم حول الارض و تعرفان حسب درجتهما بالنسبة لمرجع مطلق للزوايا ..
_ نقطتي الحضيـض و الأوج بالنسبة للمدارات الاهليلجية
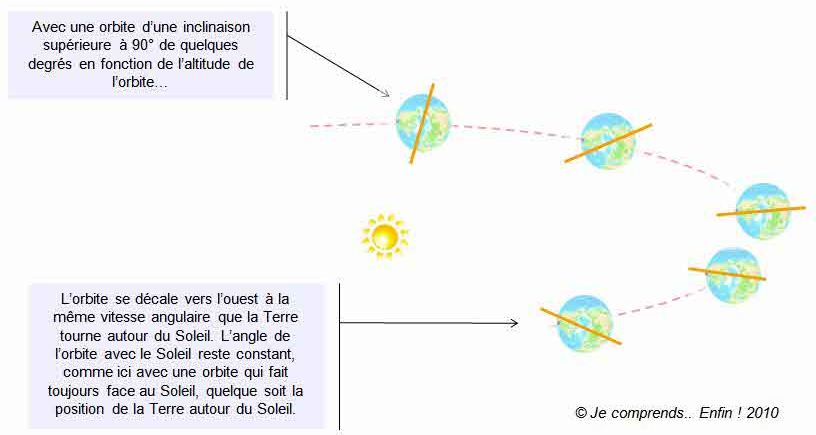
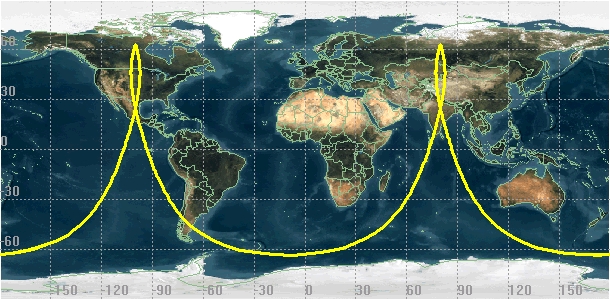
_ الاختلالات الثقـالية :من اهم ظواهر الاختلالات المدارية و تلاحظ بشكل كبير لدى المدارات شبه القطبية و ذات الميل الكبير حيث ان العقد الصاعدة و النازلة للمدار تتغير ، و درجـة الاختلالات تكون مرتبطة بشكل مباشر بارتفاع المدار و ميله المداري.. و هي ناجمة عن شكل الأرض المسطح عند القطبين و التوزيع غير المتجانس للكتلة الارضية ما يجعل قيم الجاذبية تتغير مؤثرة بالتالي على حركة الاقمار الصناعية ، و هو ما يترجم بظاهرة المداورة العقدية Nodale Precession و تغير موضع الحضيض للمدارات ذات الانزياح الكبير، و هو ما يلزمه شرح أكثر لاحقا عند الحديث عن المدار الشمسي المتزامن SSO و مدارات Molniya
نــوافـذ و محطـات الإطـلاق :
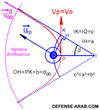
لإنجـاح إطلاق نحو مدار معين يجب الأخذ بعين الاعتبار متغيرين أساسيين ، الأول هو المدار بمختلف مميزاته و الذي سيدور فيه القمر الصناعي ، و الثاني هو مسار قاعدة الإطلاق و التي تدور بدورها مع دوران الأرض و لا يمكن الاطلاق إلا عند تقاطع إسقاط مسار المدار مع مسار قاعدة الاطلاق حول خط عرضها، كما أن توقيت الاطلاق عامل مهم .. كل هذه المعطيات هو ما يسمى : نافذة الإطلاق ، و هو ما سنتطرق اليه بتفصيل اكثر تاليا :
أ) التوقيت الفلكي المحلي Sideral Local Time
عند حساب العقد المدارية يكون من الأجدى الاعتماد على صيغة التوقيت الفلكيSLT المعتمد على دوران الأرض في مرجع مطلق عوض حسابه بالساعات و بالتالي نستعمل درجات دوران الارض فلدينا 360° في 24 ساعة فلكية و منه فان ساعة واحدة = 15 °
نحسب درجات دوران الارض بالنسبة الى نقطة مرجعية ساكنة في الفضاء تسمى Vernal Point و يرمز لـها بـ I حيث يتم اختيارها بشكل اعتباطي حسب تموضع نجوم بعيدة و ساكنة بالنسبة للأرض لتوفير أكبر نسبة من الدقة في القياس .. في وقت معين موقع قاعدة الاطلاق يتم حسابه انطلاقا من النقطة المرجعية بالدرجات ، حيث يتغير موقعها على مدى اليوم مع دوران الارض حول نفسها ..
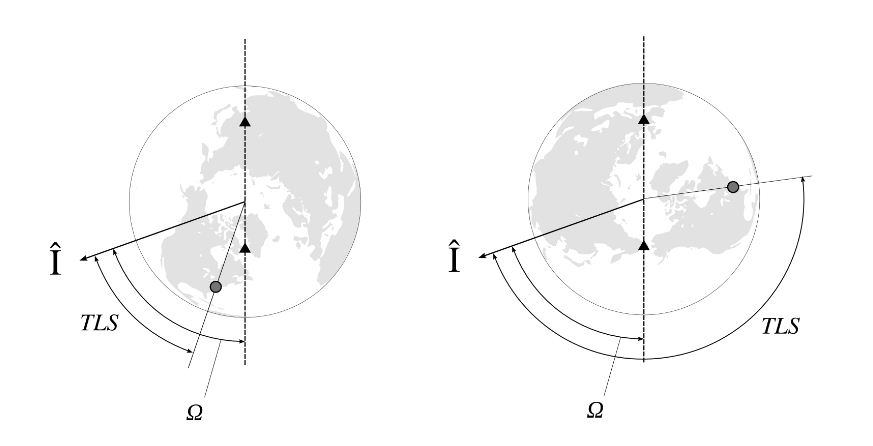
للإشارة فـإن القيمة الحقيقية لـ 24 ساعة فلكية تساوي بالتحديد 23 ساعة 56 دقيقة و 4 ثواني
ب) حالات التقاطع
مسـار المدار المفترض حول الأرض يعتمد على زاويتين و هما Ω: خط طول العقدة الصاعدة او بمعنى آخر التوقيت الفلكي عند تقاطع المدار مع مستوى خط الاستواء و التي تحسب انطلاقا من مرجع التواقيت .. الثانية هي α و هي درجة الميل المداري للمدار المفترض Inclinaison ..
من ناحية اخرى فبحسب خط عرض محطة الاطلاق Lat و درجة الميل المداري α يكون لدينا نافذة واحدة أو نافذتان أو قد لا تكون لدينا اي نافذة اطلاق مباشرة ..
عنـد α < Lat لا يكون هناك أي تقاطع بين الاسقاط الارضي لمسار المدار مع مسار محطـة الاطلاق و منـه فإنه لن توجد آنذاك أي نافذة إطلاق مباشرة و سيبقى الحل الوحيد لوضع القمر في مداره هو إطلاقه في مدار مؤقت ثم عمل مناورة مدارية تمكنـه من الوصول الى المدار المرغوب و لكنها عادة ما تكون مكلفة من ناحية الحصيلة الطاقية و كمية الوقود اللازم حرقها لتنفيذ المناورة ..
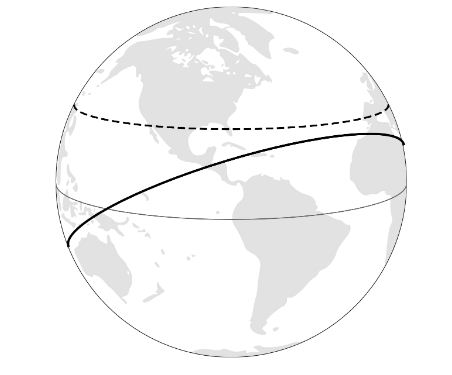
عند α = Lat
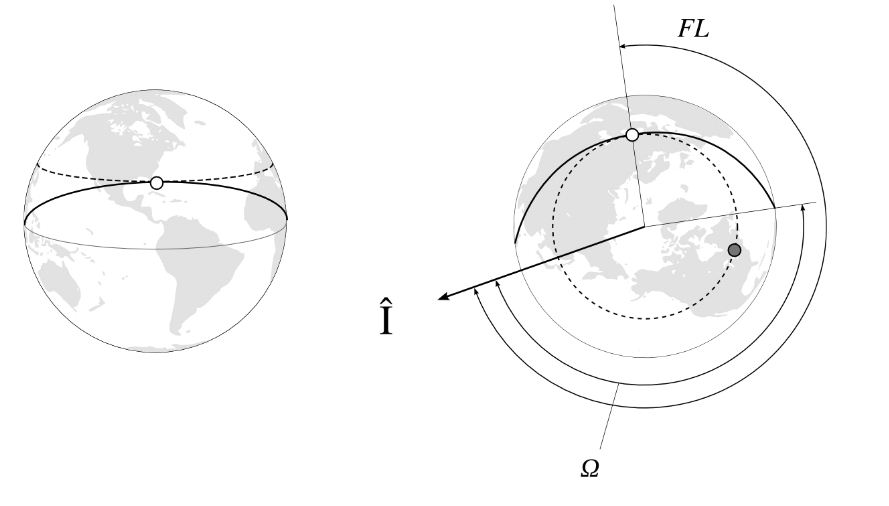
يتقـاطع المساران في نقطة وحيـدة تسمى نافذة الاطلاق FL و التي يمكن حسابها بالدرجات او بالتوقيت الفلكي المحلي حيث أن
FL= 90˚ + Ω
عندما تصل قيمة SLT الخاص بالقاعدة الى قيمة FL يكون قد حان وقت الإطلاق و في هذه الحالـة يتم الاطلاق عادة نحو الشرق مباشرة ..
عنـد α > Lat نكون أمام نافـذتي اطلاق FL 1 & FL 2 و حسابهما يتطلب بعض المعرفة بقواعد الحساب المثلثي الفلكي ، حيث يتم الامر كالآتي :
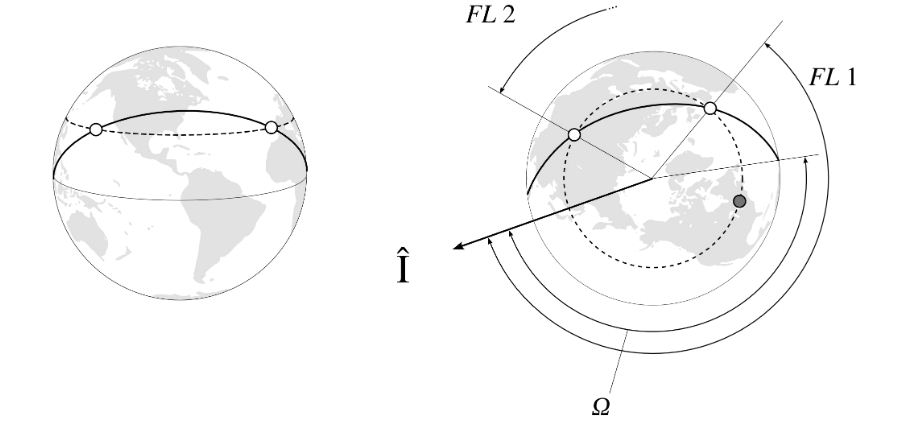
كما نرى في الـرسم التوضيحي فإن الزاوية الفاصلة بين FL 1 و Ω ليست 90° كما في الحالة السابقة إنما بينهما زاوية تدعى δ و لدينا التعبير التالي :
FL1 = δ + Ω
لحساب δ و حسب ما هو مبين في الصورة التوضيحية نجد المثلث الفلكي قائم الزاوية :
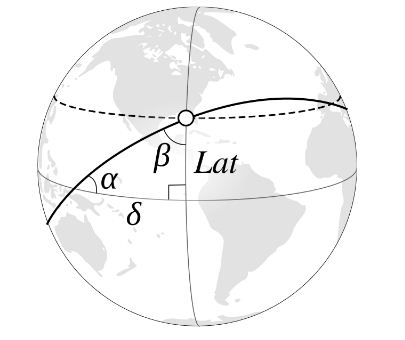
حيث δ إحدى أضلاعه ( جزء من خط الاستواء) بينما الزاوية Lat ضلعه الآخر المتعامد عليه ، و الزاوية β هي زاوية السمت Azimuth بين الشمال و مسار المدار و α الميل المداري للمدار .
العلاقتـان التاليتان تجمعان بين هذه الزوايا حسب معادلات Gauss للحساب المثلثي الفلكي :
Cos δ = Cos β / Sin α (1
سيكون علينا الآن معرفة زاوية السمت β و التي نجدها كذلك :
Sin β = Cos α / Cos Lat (2
حين تحسب كل هذه الزوايا يصبح حساب LW 1 ممكنا و بحسابه نجد نافذة الاطلاق الثانية LW2بسهولة أكثر عبر العلاقة التالية :
LW2 = LW1 + 180˚ ̵̵ 2δ
من خلال معـرفة التعابير العامة لنوافذ الاطلاق يمكننا معرفة تواقيت الاطلاق للمدارات المتوخى الاستقمارعليها انطلاقا من قاعدة إطلاق معينـة ، فـكيف يتم اختيار أمكنة انشاء قواعد الاطلاق و على اي أساس ؟
ج) قواعــد الإطلاق في العالم و مميزاتها :
قـواعد الإطلاق الفضائية و مواقعها لا تكون اعتباطية أبدا ، فالارض تدور 360˚ في 24 ساعة فلكية و بالتالي فالسرعة الخطية التي يدور بها سطحها هي :
V = W.R.Cos(Lat)
W السرعة الزاوية للأرض ، R شعاع الأرض ، Lat خط عرض المحطـة
Cos دالة جيب تمام الزاوية
و منه فكلما كان خط عرض الموقع صغيرا ( يعني أقرب لخط الاستواء) كلما تمت الاستفادة من سرعة دوران موقع الاطلاق، فالقيمة القصوى لسرعة سطح الارض عند خط الاستواء تقدر بـ 465 m/s بيـنما تكـون منعدمة عند مركزي القطبيـن ، و لذلـك فقبل إقلاع الصاروخ و الذي يبدو ساكنا لمشاهد على الارض يكون له في الواقع حوالي 5.7% من السرعة المطلوبة للاستقمار على مدار استوائي منخفض إذا افترضنا اطلاقه من موقع استوائي ، هكـذا فالبنسبة لمحطة Kourouالفرنسية في غوايان 5.23° تكون هذه السرعة 463 m/s ، Cap Canaveral في فلـوريدا 28.5° سرعة 410 m/s بينما Baikonour الروسية في كـازاخستان 45.6° سرعة 310 m/s .. لهذا السبب يتم الاطلاق عادة نحو الشرق و من قواعد أقرب ما يمكن من خط الاستواء للاستفادة من السرعة الخطية للقاعدة و أيضا لفتح نوافذ الاطلاق نحو أكبر مجال من الميل المداري للمدارات بغرض الاطلاق المباشر دون الحاجة لمناورات كثيرة و مكلفة طاقيا لتعديل الميل، و من جهة اخرى نجد أن العديد من القواعد تنفتح على مساحات خالية شرقا و حتى على المحور الشمالي/ الجنوبي ( للاطلاق نحو المدارات القطبية ) و ذلك تجنبا لسقوط معززات الصاروخ و مراحل دفعه أو مخلفات انفجار الصاروخ في حالة فشل الاطلاق عـلى مناطق مأهولـة ، لذلك فهناك قواعد مطلة على ساحل شرقي كـما في Cap Canaveral في فـلوريدا و Svobodniy في روسيا و Kourou في غوايان الفرنسية ،, San Marco,Cap Musudanبينما هناك من يطل على صحراء شرقية أو منطقة جرداء فارغة كما هو الحال مع Baikonour ,Kaputsin Yar , Plessetsk ، و قاعدة Hammaguir الفرنسية غرب مدينة بشار و التي تم اقتطاعها لصالح الجزائر الفرنسية و التي أخليت عام 67 و غيـرها ..
الاستفادة القصوى من سرعة سطح الارض لا تكون إلا إن كان المدار و قاعدة الاطلاق استوائيين و الاطلاق نحو الشرق أما فعليا فالبنسبة للمدارات ذات الميل فالاستفادة من السرعة تكون جزئية لأن متجهة سرعة المدار تكون لها 3 مركبات شرقيـة و جنوبية و سرعة سمت الراس V-zenith كما هو موضح في الصورة أسفله :
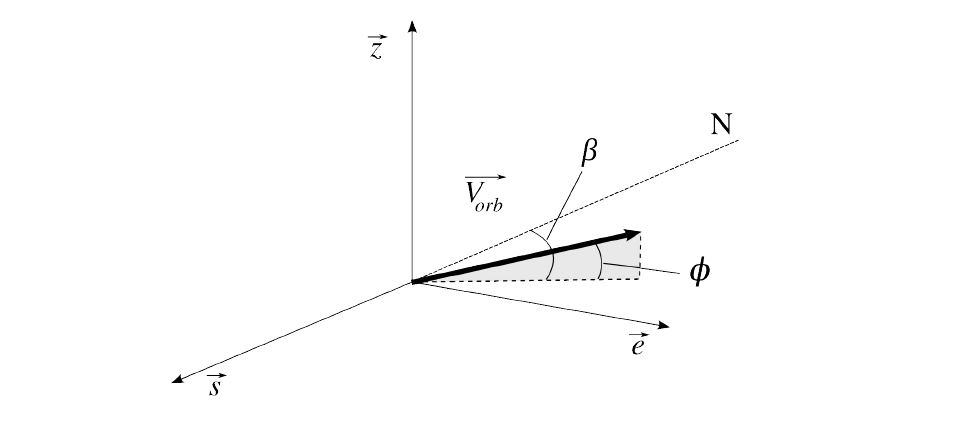
و لـذلك فنجد أن المحطات المخصصـة لإطلاق أقمار التجسس و التي تكون عادة بمدارات شبه قطبية يمكن أن يكون لها خطوط عرض مختلفة دون مشكل لأن الإطلاقات تكون نحو الشمال على مدارات تجاوز الـ 90° ببضع درجات .. مثـل Plessetsk شمال موسكو ،Jiuquan شمال الصـين ، Woomera جنوب استراليا و Vandenberg في كاليفورنيا هذه الاخيرة التي تنفتح على المحيط الهادي جنوبا و صحراء أريزونا شرقا، و تعتبر احدى أهم قواعد اطلاق أقمار التجسس الامريكية حيث يتم اطلاق أغلبها نحو الجنوب للمدارات الشبه القطبية ..
محطـة الفضاء الدولية ISS و حتى محطة Mir السوفياتية (خارج الخدمة) لهـا ميل Inclinaison 51.6° و ذلك لسبب أن الاطلاق من محطة Baikonour 46.5° يكـون في ظروف ممتازة ما يسمح لصواريخ Soyuz TMA و Proton-M مثـلا من الاستقمار بهامش من الـطاقة ، حيث يمكن استغلال ΔV التي تم اقتصادها من سرعة القاعدة و قلة التعديل المطلوب ، في زيادة حمولة الصواريخ من معدات و أجهزة لمحطة الفضاء الـدولية ..
محطــة الإطلاق العائمة Ocean Odysseyالتـابعة لشركة Sea Launch المتعددة الجنسيات هي محطة مشتقة من منصة نفط يابانية في بحر الشمال تم تحويلها الى محطة اطلاق استوائية لـغرض ايصال الاقمار التجارية و اقمار البث الفضائى الى مدار GEO بأقل خسارة طاقيـة .. المحطة تستعمل صواريخ Zenit-3 SL الاوكرانو- سوفياتية العاملة على وقود الكيروسين / الاوكسيجين السائل، حيث جرى اول اطلاق في مارس 1999 ، تتموقع الـ Ocean Odyssey قرب جزيرة Cristhmas Island في ارخبيل خط الاستواء وسط المحيط الهادئ ..
المنــاورات المـداريـة :
تكـاد لا تخلو عملية إطلاق فضــائية من مناورة لتعديل المـدار أو للانتقال من مدار لآخر سواء عبـر المرحلة النهائية من الصاروخ الحامل أو من خـلال محركات الدفع الخاصة بالأقمار الصناعية أو المسابير و المركبات الفضائية ..
مناورة Hohmann للتحويل المداري :
مدار Hohmann للتحويــل هو من الأكثر استعمالا في الانتقال بين المدارات احادية المستوى، إذ أنه أقل المناورات كلفة من الناحيـة الطاقية و يرجع الفضـل فيه الى عالم الفلك الألمـانـي فـالتر هومان Walter Hohmann منذ عشرينيات القرن العشرين ..
مناورة التحويل Hohmann هي الانتقال من مدار منخفض نحو مدار مرتفع باستعمال مدار تحويل اهليلجي حضيضه يلامس المدار المنخفض و أوجه يصل الى المدار المرتفع كما في الصـورة التوضيحية :
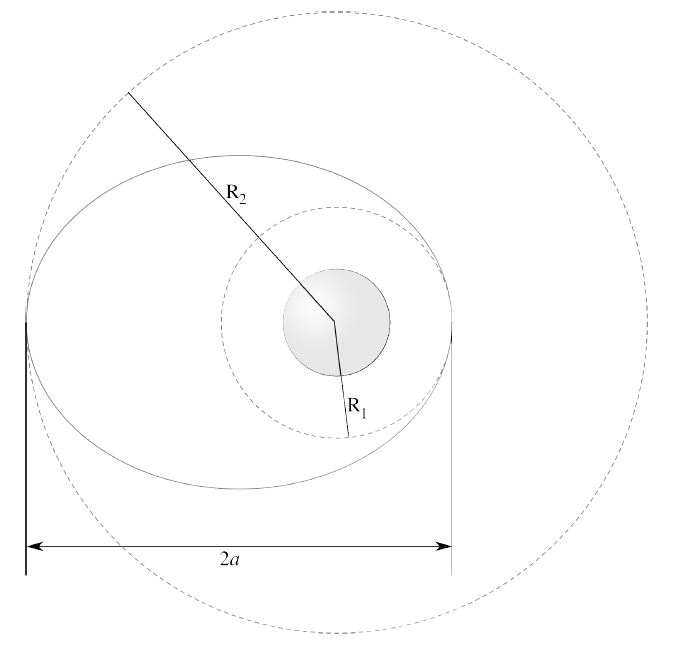
هناك مرحلتي دفع أساسيتين خلال هاته المناورة
الاولى :
دفـع على مستوى المدار المنخفض تكون متجهته مماسة للمدار ، هذا الدفع الاضافي يجعل سرعة الجسم في المدار أكبر من سرعة استقماره الدنيا التي كان يملكها قبل بداية المناورة Vs min ، ما يجعله يتخذ مدارا اهليلجيا تكون درجـة انحرافهe Orbital Excentricity مرتبطة بكمية الاضافية في أول المناورة
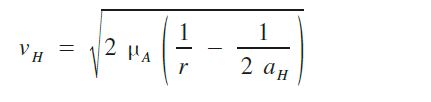
حيث aH هو نصف المحور الأكبر للاهليلج و 2aH=R1+R2 و هي المسافة الكاملة بين الحضيض و الأوج ، بينما r هو الشعاع في نقطة ما من المدار .. و منه فإنـه في أول المناورة يكون r = R1 و بالتالي يمكننا من خلال المعادلة أعلاه معرفة السرعة V(H-R1) اللازم الوصول لها في اول المناورة لبلوغ المدار ذو الشعاع R2 ..
المرحلـة الثانيـة :
أثناء الانتقال في مدار Hohmann الإهليلجي يفقد الجسم سرعته كلما ابتعد عن الحضيض ليصل الى أوج المدار بسرعة دنيا و بمسافة R2 عن الأرض ، و هي سرعة أقل بكثير من سرعة الاستقمار Vs min اللازمة ليبقى في المدار الدائري ذو الشعاع R2 ، ما يحتم اجراء دفع اضافي للوصول بالسرعة V(H-R2) الى قيمة سرعة الاستقمار في المدار المرتفع R2 ..
مناورات Hohmann لا تقتصر على الانتقال من المدار المنخفض نحو المرتفع بل يتم استغلالها ايضا في العملية العكسية .. فالمسابير و الاقمار عادة تملك محركات بدفع موجه تمكنها من العمل عكس مسار الحركة لابطاء سرعتها على مدار ما من اجل خفض ارتفاعها و النزول الى مدار أخفض ، ففي الفضاء الخارجي لا وجود للهواء و بالتالي لا يمكن اخماد الحركة الا بحركة في المنحى المعاكس ، و منه فان الحصيلة الطاقية للمناورة لا تتغير في العمليتين ..
المــوعـد المداري Spatial Rendez-Vous :
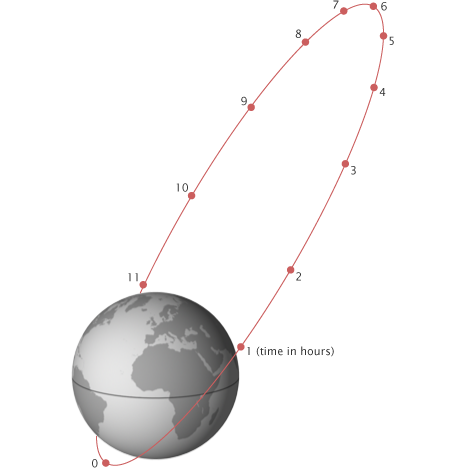
أحيـانا لا يكـون علينا الوصول الى مدار محدد فحسب بل أيضا الوصول في توقيت دقيق و هو ما يعد شيئا مهما لعمليات الالتحام بجسم في المدار المنشود أو كذلك بالنسبة لأقمار البث و الاتصالات المتواجدة على مدار Geostationnary Orbit او مدارات مولنيا.. فالموعد المداري لا يعدو ان يكون مناورة Hohmann مؤطرة في الزمن ..
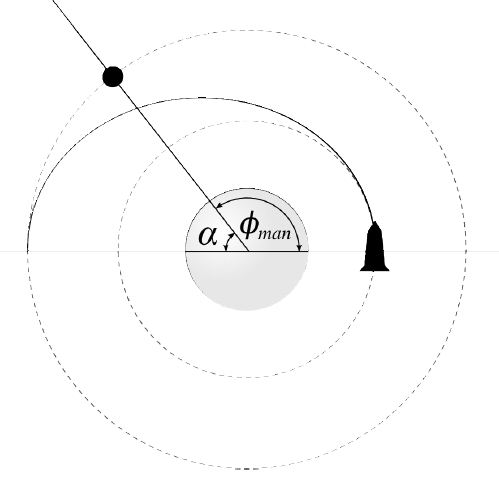
من خلال الصورة اعلاه يتضح لنا أنه للالتحام بالهدف على المدار المنشود ينبغي الانطلاق من المدار الأولي في وقت معين علينا تحديده بدقة ، هذا التوقيت يمثل تموضع المركبة بالنسبة للهدف و هو ما سنسميه زاوية الانفصال Angle of Separation و لحسابه سيكون علينا تحديد شيئين اساسيين : زمن المناورة و هو الزمن اللازم لقطع المسار نحو الهدف ، و زاوية التقدم
زمن المناورة هو بشكل اخر الوقت اللازم لقطع نصف محيط مدار التحويل الاهليلجي أي الوصول الى 180 درجة و هو يساوي نصف الدور المداري لمدار التحويل و يعبر عنه كالآتـي :
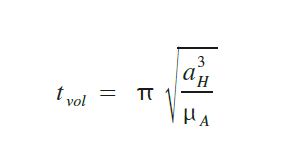
زاويـة التقدم للهدف avt α هي تغير موضعها الزاوي بالنسبة للزاوية البدئية أثناء قطع المركبة لزمن المناورة ، هذه الزاوية يمكن حسابها انطلاقا من السرعة الزاوية ω cible للهدف بشكل بسيط :
α = ω . t vol
بهذا الشكل سنستطيع حساب زاوية الانفصال maneuver Φ، هذه الزاوية التي يجب أن تفصل الجسم عن الهدف عند بداية المناورة المرجوة للالتقاء :
Φ = 180 -α
الجسمين في مدارين مختلفين ليسا تابثين بالنسبة لبعضهما و سرعتهما الزاوية تختلف حسب اختلاف مداريهما ما يجعل الزاوية الفاصلة بينهما متغيرة و لا تساوي دائما زاوية الانفصال .. من هنا جاء مفهوم وقت الانتظار و هو الوقت الذي ينبغي انتظاره من الجسم حتى يدخل في المناورة و بالتالي علينا انتظار وصول قيمة Φ initial الزاوية الفاصلة البدئية الى قيمة Φ maneuver ضمن زمن انتظار t (attente) :
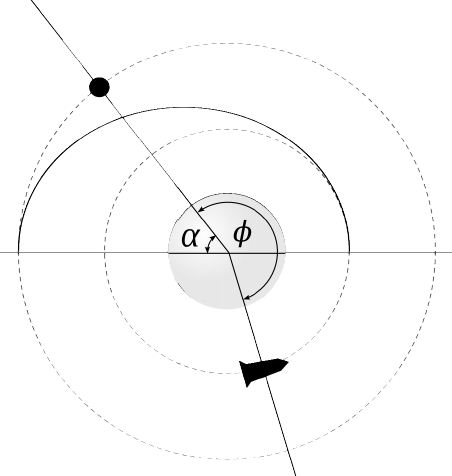
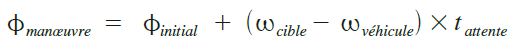
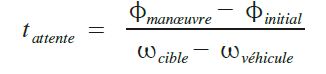
فـي حـالة Φ initial > Φ maneuver سنقع في قيمـة سالبـة لكن بما أن الظاهرة دورية فيكفي زيادة 360 لفرق الزوايا للحصول على النتيجة المقبلة الصحيحة ..
--------------------------------------
المرفقات
التعديل الأخير: